Moorish 8-4 is a chainmaille weave that I invented in 2016. If you are familiar with both the Moorish Rose weave (the parent weave of Moorish 8-4) and the idea of convex (semi)regular tilings of the plane then the weave can be described as “Moorish Rose but you are tiling with octagons and squares rather than hexagons.”

But I suppose you may want a bit more detail, so you can read this post.

Aspect ratio

If you want to make Moorish 8-4, I recommend to use 18g wire for all rings in this weave. The octagons should have AR 8.0 (3/4" or T18 using Blue Buddha Boutique’s excellent ring naming conventions), and the squares should have AR 6.0 (13/64" or M18).

You’ll have a much easier time if you use two different colors of rings; as pictured above, I’m a fan of copper squares and aluminum octagons.

Moorish Rose is a hexagonal tiling of the plane

Also in 2016, I wrote an article on mailleartisans.org about how Moorish Rose is a hexagonal tiling of the plane. Here is a brief summary in case you don’t want to read the entire thing:

• Each Mobius ball unit is a hexagon
• Each ring in the unit corresponds to one vertex
• Each set of two consecutive rings in the unit (or the “space between two vertices”) corresponds to one edge
• Each vertex in the tiling consists of 3 mutually-intersecting rings, one from each of the 3 hexagons incident to that vertex
  • these 3 rings are not the same as the triangle that visually looks like the vertex
  • rather it’s the 3 rings that “hug” the triangle
• Each edge in the tiling consists of 4 rings, two from each of the two hexagons incident to that edge
• Each hexagon unit is adjacent to 6 other hexagon units, along one edge and two vertices each

Requirements for a tiling to be possible with a Moorish Rose variant

Vertices are degree 3

Every vertex in the tiling must have degree 3, i.e. there must be 3 edges incident to it AKA there must be 3 mutually-adjacent faces that all meet at it.

For example, this tiling (which is Moorish Rose) is ok:

This tiling is not possible, because 4 faces meet at each vertex:

The tiling must be edge-to-edge

For example, this tiling has 3 faces meeting at each vertex, but it is not possible to make because it is not edge-to-edge (the 4 sides of each yellow square all touch 2 different adjacent polygons each):

Another way to describe this requirement is that the graph-theoretic edges must 1:1 correspond with the sides of the visible polygons.

Non-requirements

The following are not requirements:

• The tiling does not have to be regular or semiregular
• Indeed, the tiling does not have to be a tiling; it’s possible to create three-dimensional icosahedra by adding 20 vertices with degree 5 at evenly-spaced triangular intervals throughout Moorish Rose
• The polygons do not have to be regular, although irregularity is only possible up to a point; especially with larger ring sizes, it’s possible to deform individual units somewhat significantly.

Here are some 3-dimensional solids made using the Moorish Rose weave made by me:

And here is a radial tiling that involves some irregular hexagons (although the weave deforms a bit and the decahedra deform more than the hexagons):¹

The tiling of Moorish 8-4

All that said, Moorish 8-4 does represent a semiregular tiling of the plane, and all polygons are regular.

This is the tiling:

There are two polygons, octagons and squares. Each octagon is adjacent to 4 other octagons and 4 squares, and each square is adjacent to 4 octagons.

Making Moorish 8-4

Moorish 8-4 is most easily constructed in diagonal lines according to the picture above, starting with a row of octagons. You will first construct one row of 8-ring Mobius units, using exactly the same technique as when making the first row of Moorish Rose, the only difference being a larger AR for the rings (8.0 instead of 7.0) and more rings per unit (8 instead of 6).

Let’s label the polygons like so:

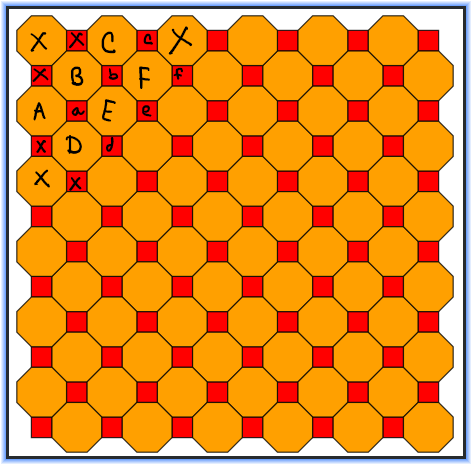
In this labeling:

• octagons have capital-letter names A, B, C, etc
• squares have lowercase-letter names a, b, c, etc
• shapes that will not appear in our weave at any time are marked with an x (non-exhaustively)

We have thus far created octagons A, B, and C. We will now create square a (once you’re comfortable with this weave, you could choose to make octagon D first to start off this row, but it’s a bit easier to start with square a). The technique here is again identical to the technique of starting the 2nd row of Moorish Rose.

Let’s call the rings/vertices in each shape 1-8 for the octagons and 1-4 for the squares. Rings that are not yet intersecting anything are all identical, but once they intersect another face they become distinguishable,² so we’ll use the convention that the rings are ordered 1, 2, 3, etc starting from the left of the bottom two corners, so A5 and A6 intersect B1 and B2.³ (Note, until we weave a ring from square a, A5 and A6 are interchangeable with each other; and B1 and B2 are interchangeable with each other.)

We now have the tools needed to describe the intersection pattern of all rings in square a:⁴

1. Weave a2 through A7 then B1 then A6 then B8
2. Weave a1 through A7 then A6 (then a2)⁵
3. Weave a3 through B1 then B8 (then a1 and a2)
4. Weave a4 through (a1, a2, and a3)

Next, octagon D:

1. Weave D4 through A8 then a4 then A7 then a1
2. Weave D3 through A8 then A7 (then D4)
3. Weave D5 through a4 then a1 (then D4 and D3)
4. Weave the rest of the rings through (D3, D4, and D5)

The rest of the weave follows from here. All octagon rings will intersect exactly two rings from one other octagon and exactly two rings from one other square, and all square rings will intersect exactly two rings from each of two adjacent octagons.